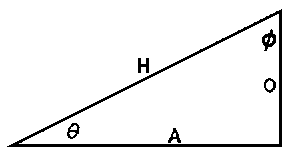
| In any right triangle, if we let | |||||||
| Ø | = | the acute angle formed by the hypotenuse and the base leg, |
|||||
| ø | = | the acute angle formed by the hypotenuse and the altitude leg, |
|||||
| H | = | the hypotenuse, | |||||
| A | = | the side adjacent Ø and opposite ø, | |||||
| O | = | the side opposite Ø and adjacent ø, | |||||
| then | sine of Ø | = | sin Ø | = | O/H | ||
| cosine of Ø | = | cos Ø | = | A/H | |||
| tangent of Ø | = | tan Ø | = | O/A | |||
| cosecant of Ø | = | csc Ø | = | H/O | |||
| secant of Ø | = | scc Ø | = | H/A | |||
| cotangent of Ø | = | cot Ø | = | A/O | |||
 |
|||||||||
| also | |||||||||
| sin Ø | = | cos ø | csc Ø | = | sec ø | ||||
| cos Ø | = | sin ø | scc Ø | = | csc ø | ||||
| tan Ø | = | cot ø | cot Ø | = | tan ø | ||||
| and | |||||||||
| 1/sin Ø | = | csc Ø | 1/csc Ø | = | sin Ø | ||||
| 1/cos Ø | = | sec Ø | 1/sec Ø | = | cos Ø | ||||
| 1/tan Ø | = | cot Ø | 1/cot Ø | = | tan Ø | ||||
| The expression “arc sin” indicates, “the angle whose sine is”…; like wise arc tan indicates, “the angle whose tangent is”…etc. See formulas in table below |
|||||||||
| Known Values |
Formulas for determining Unknown Values of … | |||||
| A | O | H | Ø | ø | ||
| A & O | 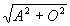 |
arc tan O/A | arc tan A/O | |||
| A & H | 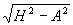 |
arc cos A/H | arc sin A/H | |||
| A & Ø | A tan Ø | A/cos Ø | 90° – Ø | |||
| A & ø | A/tan ø | A/sin ø | 90° – ø | |||
| O & H | 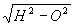 |
arc sin O/H | arc cos O/H | |||
| O & Ø | O/tan Ø | O/sin Ø | 90° – Ø | |||
| O & ø | O tan ø | O/cos ø | 90° – ø | |||
| H & Ø | 90° – Ø | |||||
| H & ø | 90° – ø | |||||
